为什么会产生负数

自然物质界本身是没有负数概念的，但到了人文世界，一种约定出现，满足需求的差值就是负数。五个人只有3份饭，那就差2份。
在不同的时间发现这个差值，有不同的处置办法。
原计划3人份饭，可来了5个需要吃饭的人，只好赶快补足了事。
原来知道有5个人，只准备3份饭。其用心就需要度量了。
第一简单来说,是为了解决数学上方程式无解的尴尬问题,众所周知,当一元二次方程判别式小于0时,方程无解.为了解决这个问题,提出了虚数的概念,令 i的平方等于-1,那么就解决了方程式的问题,也解决了很多实际问题,而复数就是.
第二
5＋√－15＝5＋√15i这种表示方法是卡尔丹发明的。这种表示称复数
第三表示学术研究的学科门类一般都是拉丁语词，以-ics结尾。math=maths=mathematics，physics，politics，linguistics
第四我只能说怎么多了！谢谢你的
收入是正，花掉是负
【为什么会产生负数】正因为有正数，才会产生負数。正数和負数是人类的哲理逻辑，阴阳的对立面。正、負的中间是O 。农村盖房时常说正負零，正是老台以上是正，負是台面以下。这个零就是易学中的无极，可見我们的老祖对这些早有定論。

秒懂知识为您整理更多相关内容。
随着人类历史的发展，有一些比0更不可思议的数字开始在欧洲流行起来了，它们是一些比0还小的数字，被称作负数。要知道，0的存在就已经很让人抓狂了，怎么会有比0还小的数字呢？是什么人吃错了药，非要使用这样的数字呢？商人！那他们使用负数有什么好处呢？赚钱！什么？赚钱？负数为什么会让商人多赚钱呢？要想知道这一点，我们首先就要弄明白，商人是怎么赚钱的：
大家都知道，所谓商人，就是靠倒卖东西赚钱的人，他们以很便宜的价格把货物从产地买进来，再以昂贵的价格在市场上卖出去，从中赚取差价。一个商人要想赚钱，首先必须要拥有一笔启动资金，先用这笔钱买来货物，然后再卖出去才能赚钱。假设一开始这个商人只有10万元，那么，他就只能先买进10万元的货物，如果他把这些货物卖出以后能收入15万元，那么，他买卖一次货物，就能赚5万元钱。我们再假设他买卖一次货物需要1个月的时间，这就意味着他1个月的时间就能把10万变成15万，让自己的资产翻1.5倍。那么，如果他一开始就有100万呢？他就可以一次进100万元的货物，而1个月后，他的资产翻1.5倍，就会变成150万。换句话说，商人赚钱的多少，是受他的成本控制的，越是有钱的商人，赚钱越快。可是这件事跟负数有什么关系？说来说去，我们得到的结论不就是一句废话吗，谁不知道越有钱的人赚钱越容易呢。
不对！刚才的这些内容啊，都是理论分析，如果你去市场上观察你会发现：商人能进的货，远远比他手里的现金要多，一个手里只有10万现金的商人，就能做着100万的生意。为什么？因为他在这个市场上经营的时间长了，跟客户和供货商的关系特别好，于是他们彼此之间产生了相互的信任关系，因此大多数生意都是在相互赊欠的情况下完成的。虽然我手里只有10万现金，但是我还有很多客户，他们欠着我80万的账款，同时，我的仓库中还有10万的货物，在这种情况下，我就可以毫不费力的从进货商那里再赊来90万的货物，等我把货物卖出去，把钱赚到手以后，再慢慢的还给他们。在一个稳定成熟的市场上，商人之间比拼的不仅是谁手中的现金多，更是谁的信用更好，信用多的人就能够赊欠更多的货款，所以他的生意就能做的更大。一个毫无信誉的人，手里有20万现金，他就只能同时做20万的生意，而一个信誉良好的人，手里有10万现金，却可以同时做100万的买卖。那么，欠债经营这件事是不是临时的呢，一个商人如果靠着欠债赚回100万了，我是不是就可以不用欠别人的钱了呢，不是的，如果他有100万现金，他就有资格欠别人1000万了，他也就可以同时开始做1000万的生意了。
从上面的分析中可以看到，债务是一个商人信用的表现，依靠债务，商人可以扩大自己的生意规模，让自己多赚十倍的利润。因此欠债在商业活动中是一种常见的现象。那么，我们要如何在账面儿上同时体现出来现金和负债呢？有人说，我可以通过欠款两个字来表示，也有人说，我可以用不同颜色表示，比如用黑色的字表示收入，红色的字来表示负债。这些办法当然可以，但是，更为简便的办法是直接使用负数。负数是比0还小的数，它代表的含义与正数的含义相反。就在商人们开始大量的使用负数的时候，在一些数学家的笔下，负数也出现了：
我们都知道，加法是具有交换律的，比如3+5的结果和5+3的结果是一样的，这一点在人类发现加法的时候，就已经知道了，因为加法代表的就是两个数的和，而相加的结果与两个数字出现的顺序是无关的。但是，人们也知道，与加法相反的减法显然是不符合交换律的，5-3显然和3-5有着本质的区别。但是，如果你的算式中多了一个数字，比如，如果你的算式是7-3+2，你就会发现，无论是先-3，还是先+2，结果总是不变的，7-3+2=6,7+2-3也是=6的。当然，这样的算式还可以t有无限多个，算式也可以无限的长，只要你不把减号后面的数挪到第一个数字的位置上去，无论你怎么移动后面加减的数字，最终的得数总是不变的。这就奇怪了，为什么减法有时候可以交换，有时候不能交换呢？为什么第一位的数字就这么特殊呢？其实不只是第一个位置特殊，人们发现：类似2+5-3这样的算式也是特殊的,它的结果等于4，但-3却不可以随便的移动，如果你把-3移动到中间，变成了2-3+5，前面的2-3，也就没有意义了。这个矛盾引发了一些数学家的思考，大家普遍认为，如果我们做一个规定，规定小数减去大数等于一个负数，那么，这个算式自然就有意义了，比如如果规定2-3=-1,那么-1+5就等于5-1,结果同样是等于4 。于是，负数就作为一种临时运算的中间结果被保留了下来。值得注意的是，虽然负数的实际应用早就产生了，但是几乎所有的数学家都坚持认为负数是没有任何实际意义的，它只是一种为了运算方便而增加的临时概念。这种观点一直延续到近代，在笛卡儿建立坐标系的时候，还是把负数当假数，甚至连18世纪的欧拉也深信不疑，一直到了19世纪，摩尔根等人还说：负数的存在是“十分荒谬”的。
那么，是什么原因让大家普遍接受了负数呢？其实，是一种全新的世界观。过去，我们之所以认为最小的数字是0，那是因为我们认为这个世界上，一切跟数字相关的量都是有起点和终点的。比如人的年龄即不可能小于0，又不可能是无限大。同时，任何一方土地，无论它多么广阔，它也是有边界的，如果我们设定一块土地的最左侧表示0，那么从左到右的测量下去，总会有一个数字表示土地的长度和宽度。但是，随着我们对整个宇宙的认识的不断深入，人类的视野逐渐开阔起来，我们总是能发现距离我们更加遥远的星系，在这个过程中，人类逐渐感受到，整个宇宙空间似乎是没有边界的，与之对应的时间似乎也是没有起点、没有终点的。像时间和空间这样没有起点的量，我们就没有办法用0表示它诞生的时刻，或者它开始的地方。因此，我们就只能从中取一个表示0的点，而后用正数和负数分别表示两个不同方向的量。比如，我们用0年表示公元元年，在此之后的年份就用正数表示，而在此之前的年份用负数表示。再比如，地球的经度，我们也只能人为约定格里尼治天文台的经度为0，自此向东用正数表示，自此向西用负数表示。另外，一开始我们认为，像温度这样的量，也是没有最小值的，因此，我们就约定水结冰的温度为摄氏0度，高于0度的用正数表示，低于0度的用负数表示。尽管后来我们发现温度是存在最小值的，它的最小值被称为绝对0度，然而由于绝对0度的环境太不常见了，所以我们还是保持了原来的习惯。
这样一来，负数的存在就有了与之对应的实际含义，于是负数的概念就被世人广泛接受了。

数的产生和发展离不开生活和生产的需要。自然数是在人类的生产生活实践中产生的。与之相比，负数的产生则是经历了一个更为漫长的过程。

文章插图
中国是世界上首先使用负数的国家
战国时期，李悝（约公元前455—前395）在《法经》中说：“衣五人终岁用千五百不足四百五十”，其意思是说，5个人一年开支1500钱，入不敷出，尚“不足四百五十”，即还差450钱。这里的“不足”就是负数的意思。
负数概念最早出现在我国的《九章算术》中，里面提出了正负数加减法则，但未说明什么是正负数。
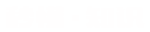
据史料记载，早在两千多年前，我国就有了正负数的概念，掌握了正负数的运算法则。人们计算的时候用一些小竹棍摆出各种数字来进行计算。这些小竹棍叫做“算筹”算筹也可以用骨头和象牙来制作。
我国三国时期的学者刘徽在建立负数的概念上有重大贡献。刘徽首先给出了正负数的定义，他说：“今两算得失相反，要令正负以名之。”意思是说，在计算过程中遇到具有相反意义的量，要用正数和负数来区分它们。刘徽第一次给出了正负区分正负数的方法。他说：“正算赤，负算黑；否则以邪正为异”意思是说，用红色的小棍摆出的数表示正数，用黑色的小棍摆出的数表示负数；也可以用斜摆的小棍表示负数，用正摆的小棍表示正数。

文章插图
据有关资料显示，负数的产生与其他数学概念的形成相类似。负数是为了表示并计算现实生活中具有相反意义的量。当生活中用单一的数概念无法准确地描述两种迥然不同的量时，人们自然想到了扩充原有的数概念以适应新的需要。
有关这方面内容的文字记载据说最早出现在《九章算术》中。关于负数的引入,书中以卖（收入钱）为正,买（付出钱）为负；余钱为正,不足钱（亏钱）为负；在关于粮谷计算的问题中,益实（增加粮谷）为正,损实（减少粮谷）为负。
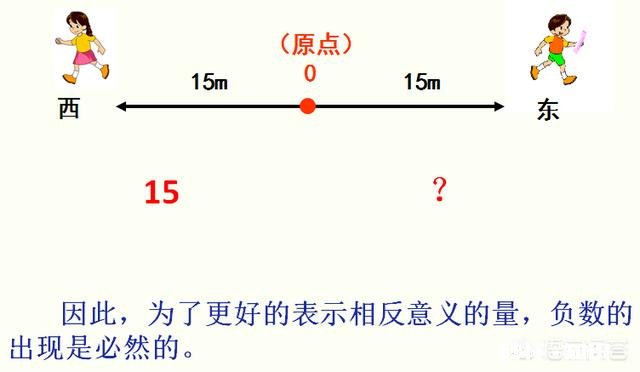
我们来看两个生活中的例子吧。

文章插图

文章插图
但是相反意义量的存在并不是负数产生的充分条件。换句话说，有了负数，确实有利于表示相反意义的量；但并不是说没有负数，就不能表示相反意义的量，如果我们在同一个数的前面注上两个反义词，问题不也就解决了吗？
是的，在《九章算术》中的直除法消元，必然会出现零减去正数的情况，要使运算进行下去，必须引进负数。

文章插图

因此，正负是相对的。在列方程时可以根据消元的方便确定各行的符号。正负是两种不同的运算，加上一个正数等于减去一个负数，加上一个负数等于减去一个正数，这样，运算便可畅行无阻。
《九章算术》中引入这些实际的例子很好地说明了古代先哲是如何提出负数的。或许对你理解负数是如何诞生的也有所启发。

文章插图
负数在国外出现的理由及发展状况
尽管中国古人首先发现并应用了负数，但客观地说，算法中使用负数和在逻辑上真正理解负数是两个层面的事情。负数的数学意义，首先是西方数学家们建构起来的。
在西方，人们认识负数比认识无理数还困难。被誉为代数学鼻祖的希腊数学家丢番图（246-330）虽知道把“负负得正，正负得负”的乘法法则运用于（x-1）（x-2）一类的乘法，但他认为2x<10是荒谬的。
在公元1150年（比《九章算术》成书晚1千多年），印度在公元7世纪才采用负数，公元628年，印度的《婆罗摩修正体系》一书中，把负数解释为负债和损失，是西方最早在数学上使用负数的是一本印度数学文献。它的出现是为了表示负资产或债务。在很大程度上，欧洲数学家直到17世纪才接受负数的概念。

文章插图

13世纪初，意大利数学家斐波那契解释负数为“欠款” 。15世纪，法国数学家许凯在1484年对解方程中多次出现的负数解用赊欠等词语解释了它们的意义。
著名的德国数学家史提非在1544年说负数是“无稽的”或“虚伪的零下。16世纪法国数学家韦达解方程时仍然不要负数。1545年，意大利的卡当著《大法》，成为欧洲第一部论述负数的著作。
法国数学家吉拉尔在《整数算术》中正式用“+”、“-”表示加、减，并注意到负数不单是一种减数，还是小于零的数，比零小也就是“小于一无所有”，因而负数是“荒谬的数” 。”这样的表示方法被广泛接受，并沿用至今。
特别是1637年，法国数学家笛卡尔发明了解析几何学，建立了坐标点，将平面点与负数、零、正数组成的实数对应起来，使负数得到了解释，从而加速了人们对负数的承认。
直到1712年，连莱布尼兹也承认这种说法合理。英国数学家瓦里承认负数，同时认为负数小于零而大于无穷大（1655年）。他对此解释到：因为a＞0时，英国著名代数学家德。摩根在1831年仍认为负数是虚构的。
但直到19世纪，德国数学家魏尔斯特拉斯等人为整数奠定了逻辑基础以后，负数才在现代数学中获得巩固的地位。

文章插图
一点感慨
从上面可以看出，负数的引进，是我国古代数学家贡献给世界数学的一份宝贵财富。单、但东方数学的发展满足于解决问题，所以对负数的认识只限于它的四则运算，直至近代也没有更多的的突破。西方对负数的探讨虽然起步较晚，但理性思辨的传统，使得他们从一开始就聚焦于方程负数解的讨论上，并最终完成了对负数的数学抽象。